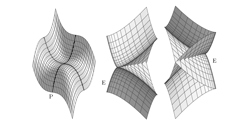

Abstract:
It is shown that curves and surfaces with a linear field of normal vectors are dual to graphs of univariate and bivariate polynomials. We discuss the geometric properties of these curves and surfaces. In particular, it is shown that the convolution with general rational curves and surfaces yields again rational curves and surfaces.
Bibtex:
@article{sampoli-2005-epcs,
author = "M. L. Sampoli and M. Peternell and B. J{\"u}ttler",
title ="Rational surfaces with linear normals and their
convolutions with rational surfaces",
journal = "Comput. Aided Geom. Design",
volume = 23,
year = 2006,
pages = "179-192",
url="/peternell/lnsurf.pdf"
}
|
|