
Abstract:
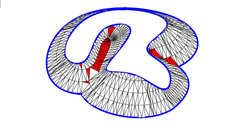
Given a closed plane curve c(t) = (c1,c2)(t) Π² and associated function values g(t) we present a geometric idea and an algorithm to solve the equation ||Ñf|| = a = const. with respect to the boundary values g(t) along the boundary c(t).This is equivalent to finding a developable surface D of constant slope a = tana through the spatial curve C determined by (c1,c2,g)(t). The presented method constructs level curves of the surface D. We put some emphasis on the treatment of the singularities of the solution which are D’s self intersections.
Bibtex:
@inproceedings{peternell-2005-ee,
title = "A geometric idea to solve the eikonal equation",
author = "Martin Peternell and Tibor Steiner",
booktitle = {SCCG '05: Proceedings of the 21st spring conference
on {C}omputer graphics},
editor = "Bert J{\"u}ttler",
publisher = "ACM Press",
ISBN = "1-59593-203-6",
pages = "43-48",
year = 2005,
url="/peternell/eikeqn.pdf",
doi="10.1145/1090122.1090130",
alternatepages = "41-46",
alternatepublisher = "Comenius University",
alternateaddress = "Bratislava",
alternateISBN = "80-223-2057-9",
}
|
|