|
Welcome to the research group
Differential Geometry and Geometric Structures
|
|
Members & friends of the group in Jul 2021
photograph © by Narges Lali
|
Differential geometry has been a thriving area of research
for more than 200 years, employing methods from analysis
to investigate geometric problems. Typical questions
involve the shape of smooth curves and surfaces and the
geometry of manifolds and Lie groups. The field is at
the core of theoretical physics and plays an important
role in applications to engineering and design.
Finite and infinite geometric structures are ubiquitous
in mathematics. Their investigation is often intimately
related to other areas, such as algebra, combinatorics or
computer science.
These two aspects of geometric research stimulate and
inform each other, for example, in the area of "discrete
differential geometry", which is particularly well suited
for computer aided shape design.
|
|
Gallery of some research interests and projects
Symmetry breaking in geometry:
We discuss a geometric mechanism that may,
in analogy to similar notions in physics,
be considered as "symmetry breaking" in geometry.
(Fuchs, Hertrich-Jeromin, Pember;
Fig ©Nimmervoll)
Cyclic coordinate systems:
an integrable discretization in terms of a discrete flat
connection is discussed.
Examples include systems with discrete flat fronts or
with Dupin cyclides as coordinate surfaces
(Hertrich-Jeromin, Szewieczek)
We study surfaces with a family of
spherical curvature lines
by evolving an initial spherical curve through
Lie sphere transformations,
e.g., the Wente torus
(Cho, Pember, Szewieczek)
Discrete Weierstrass-type representations
are known for a wide variety of discrete surfaces classes.
In this project, we describe them in a unified manner,
in terms of the Omega-dual transformation applied to
to a prescribed Gauss map.
(Pember, Polly, Yasumoto)
Billiards:
The research addresses invariants of trajectories of a
mass point in an ellipse with ideal physical reflections
in the boundary. Henrici's flexible hyperboloid paves the
way to transitions between isometric billiards in ellipses
and ellipsoids (Stachel).
Spreads and Parallelisms:
The topic of our research are connections among spreads
and parallelisms of projective spaces with areas like
the geometry of field extensions, topological geometry,
kinematic spaces, translation planes or flocks of quadrics.
(Havlicek)
This is a surface of (hyperbolic) rotation in hyperbolic
space that has constant Gauss curvature,
a
recent classification project.
(Hertrich-Jeromin, Pember, Polly)
Geometric shape generation:
We aim to understand geometric methods to generate
and design (geometric) shapes,
e.g., shape generation by means of representation formulae,
by transformations, kinematic generation methods, etc.
(Hertrich-Jeromin, Fig Lara Miro)
Affine Differential Geometry:
In affine differential geometry a main point of research is
the investigation of special surfaces in three dimensional
affine space.
(Manhart)
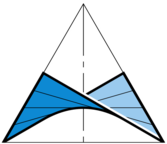
Transformations & Singularities:
We aim to understand how transformations of particular
surfaces behave (or fail to behave) at singularities, and
to study how those transformations create (or annihilate)
singularities.
The figure shows the isothermic dual of an ellipsoid,
which is an affine image of a minimal
Scherk tower.
(Hertrich-Jeromin)
|
|
News
12 Dec 2022
16 Jan 2023: Geometry seminar- Christian Müller (TU Wien):
The Geometry of Discrete AGAG-Webs in Isotropic 3-Space
Abstract
We investigate webs from the perspective of the geometry of webs
on surfaces in three dimensional space. Our study of AGAG-webs
is motivated by architectural applications of gridshell
structures where four families of manufactured curves on a
curved surface are realizations of asymptotic lines and geodesic
lines. We describe all discrete AGAG-webs in isotropic space and
propose a method to construct them. Furthermore, we prove that
some sub-nets of an AGAG-web are timelike minimal surfaces in
Minkowski space and can be embedded into a one-parameter family
of discrete isotropic Voss nets. This is a joint work with
Helmut Pottman.
- 28 Nov 2022: Geometry seminar
- Günter Rote (FU Berlin):
Grid peeling and the affine curve-shortening flow
Abstract
Grid Peeling is the process of taking the integer grid points
inside a convex region and repeatedly removing the convex hull
vertices.
It has been observed by Eppstein, Har-Peled, and Nivasch,
that, as the grid is refined, this process converges to
the Affine Curve-Shortening Flow (ACSF), which is defined
as a deformation of a smooth curve.
As part of the M.Ed. thesis of Moritz Rüber, we
have investigated the grid peeling process for special
parabolas, and we could observe some striking phenomena.
This has lead to a conjecture for the value of the constant
that relates the two processes.
- 18 Nov 2022, Zeichensaal 3: Festkolloquium
- zum 80. Geburtstag von Hellmuth Stachel
Programm
- 13:15 - 14:00
- Eröffnung und Laudatio von Otto Röschel
- 14:00 - 15:00
- Johannes Wallner (TU Graz):
Flexible nets and discrete differential geometry
- 15:00 - 16:00
- Georg Glaeser (Universität für angewandte Kunst Wien):
Forty years between descriptive and computational geometry:
the universe of spatial imagination
- 16:00 - 16:30
- Kaffeepause
- 16:30 - 17:30
- Hans-Peter Schröcker (Universität Innsbruck):
Devil in paradise II - recent results in motion factorization
- 17:30 - 18:30
- Giorgio Figliolini (Universität Cassino):
Kinematics of mechanisms with higher-pairs:
fundamentals and applications
- 19:00
- Abendessen im Restaurant Waldviertlerhof,
Schönbrunnerstr. 20, 1050 Wien
- 14 Nov 2022: Geometry seminar
- Karoly Bezdek (University of Calgary):
Ball polyhedra -- old and new
Abstract
We survey a number of metric properties of intersections of
finitely many congruent balls called ball polyhedra in Euclidean
spaces. In particular, our talk is centered around the status of
the shortest billiard conjecture, the global rigidity
conjecture, Hadwiger???s covering conjecture, and the
Gromov-Klee-Wagon volumetric conjecture for ball polyhedra.
|
Technische Universität Wien
