|
|
I3809-N32: Geometric shape generation
Joint Project between Austria (FWF) and Japan (JSPS)
|
|


|
Project leader (Austria): Udo Hertrich-Jeromin
Project leader (Japan): Miyuki Koiso
Funding period: 1 Apr 2018 - 30 Sep 2021
(approved 5 Mar 2018)
Fields: Mathematics, Arts;
Areas: Differential geometry, Integrable systems,
Discrete differential geometry, Geometric design methods
|
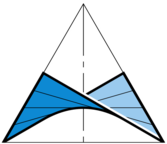
 Semi-discrete principal net,
Semi-discrete principal net,
smoothed by channel surfaces
(Fig: M Lara Miro)
|
Abstract.
Explicit classification results and representation formulae
are at the core of the differential geometry of curves and
surfaces - they serve to generate geometric shapes (curves
or surfaces) with certain prescribed properties: for example,
the classical Weierstrass representation formulae serve to
generate any surface that (locally) minimizes area out of
simple data.
Other shape generation methods include "transformations",
which transform a given shape of a certain class into
another such shape, while preserving its key properties.
While such "shape generation methods" are designed to produce
curves or surfaces of a particular kind out of suitable input
data, it is often difficult to control other features of the
generated shape by the input data - deep knowledge about the
particular shapes and the generation process are required.
These shape generation methods play an important role in
geometry, not just for the production of interesting shapes
for design or ilustration purposes, but also to obtain a
better understanding of the structure of the investigated
shapes. In particular, the properties of transformations
are essential for describing facetted or panelled surfaces
that display similar properties as the corresponding smooth
surfaces.
In this project we aim to investigate different methods to
generate shapes, in particular:
- the interrelations between different shape generation
methods;
- the related discretizations and, hence, discretizations
of the shape generation methods;
- the applicability and scope of these shape generation
methods in theory and generative art and design.
By interlinking these different aspects of shape generation
we hope and expect to gain new insight and to establish new
interesting methods for the geometric generation of shapes,
for their use in theory as well as for their application
in art or design.
|
|
Publications.
- J Cho, Y Ogata (2019)
-
Simple factor dressings and Bianchi-Bäcklund transformations;
Illinois J Math 63(4), 619-631 (2019)
DOI:10.1215/00192082-7988989
Abstract
In this paper, we directly show the known equivalence of
simple factor dressings of extended frames and the classical
Bianchi-Bäcklund transformations for constant mean
curvature surfaces. In doing so, we show how the parameters
of classical Bianchi-Bäcklund transformations can be
incorporated into the simple factor dressings method.
- S Akamine, J Cho, Y Ogata (2020)
-
Analysis of timelike Thomsen surfaces;
J Geom Anal 30, 731-761 (2020)
DOI:10.1007/s12220-019-00166-7,
EPrint arXiv:1808.09641
Abstract
Timelike Thomsen surfaces are timelike minimal surfaces that
are also affine minimal. In this paper, we make use of both
the Lorentz conformal coordinates and the null coordinates,
and their respective representation theorems of timelike
minimal surfaces, to obtain a complete global classification
of these surfaces and to characterize them using a geometric
invariant called lightlike curvatures. As a result, we reveal
the relationship between timelike Thomsen surfaces, and
timelike minimal surfaces with planar curvature lines. As an
application, we give a deformation of null curves preserving
the pseudo-arclength parametrization and the constancy of
the lightlike curvatures.
- S Akamine, M Umehara, K Yamada (2020)
-
Improvement of the Bernstein-type theorem for space-like
zero mean curvature graphs in Lorentz-Minkowski space
using fluid mechanical duality;
Proc Amer Math Soc, Ser B 7, 17-27 (2020)
DOI:10.1090/bproc/44
Abstract
Calabi's Bernstein-type theorem asserts that a zero
mean curvature entire graph in Lorentz-Minkowski space
$L^3$ which admits only space-like points is a space-like
plane. Using the fluid mechanical duality between minimal
surfaces in Euclidean 3-space $E^3$ and maximal surfaces in
Lorentz-Minkowski space $L^3$, we give an improvement of
this Bernstein-type theorem. More precisely, we show that
a zero mean curvature entire graph in $L^3$ which does not
admit time-like points (namely, a graph consists of only
space-like and light-like points) is a plane.
- S Akamine, A Honda, M Umehara, K Yamada (2021)
-
Bernstein-type theorem for zero mean curvature hypersurfaces
without time-like points in Lorentz-Minkowski space;
Bull Braz Math Soc, New Series 52, 175-181 (2021)
DOI:10.1007/s00574-020-00196-8,
EPrint arXiv:1907.01754
Abstract
Calabi and Cheng-Yau's Bernstein-type theorem asserts that
an entire zero mean curvature graph in Lorentz-Minkowski
$(n+1)$-space $\mathbb{R}^{n+1}_1$ which admits only
space-like points is a hyperplane. Recently, the third and
fourth authors proved a line theorem for hypersurfaces at
their degenerate light-like points. Using this, we give an
improvement of the Bernstein-type theorem, and we show that
an entire zero mean curvature graph in $\mathbb{R}^{n+1}_1$
consisting only of space-like or light-like points is a
hyperplane. This is a generalization of the first, third
and fourth authors' previous result for $n=2$.
- S Akamine, H Fujino (2021)
-
Reflection principle for lightlike line segments on maximal surfaces.
Ann Glob Anal Geom 59, 93-108 (2021)
DOI:10.1007/s10455-020-09743-4
Abstract
As in the case of minimal surfaces in the Euclidean
3-space, the reflection principle for maximal surfaces in
the Lorentz-Minkowski 3-space asserts that if a maximal
surface has a spacelike line segment $L$, the surface is
invariant under the $180^\circ$-rotation with respect to
$L$. However, such a reflection property does not hold
for lightlike line segments on the boundaries of maximal
surfaces in general. In this paper, we show some kind of
reflection principle for lightlike line segments on the
boundaries of maximal surfaces when lightlike line segments
are connecting shrinking singularities. As an application,
we construct various examples of periodic maximal surfaces
with lightlike lines from tessellations of $\mathbb{R}^2$.
- J Cho, W Rossman (2020)
-
Discrete isothermicity in Moebius subgeometries;
in Yang (ed): An introduction to Discrete Differential Geometry,
Anam Lecture Notes 2, 37-81 (2020)
Abstract
We give an elementary description of Möbius geometry
using a Minkowski space model, primarily in low dimensions
with comments about generalizing to higher dimensions. We
then give an application to the discretization of isothermic
surfaces in three dimensional spaceforms.
- J Cho, W Rossman, T Seno (2021)
-
Discrete mKdV equation via Darboux transformation;
Math Phys Anal Geom 24, 25 (2021)
DOI:10.1007/s11040-021-09398-y
Abstract
We introduce an efficient route to obtaining the discrete
potential mKdV equation emerging from a particular discrete
motion of discrete planar curves.
- J Cho, W Rossman, S-D Yang (2021)
-
Discrete Minimal Nets with Symmetries;
in: Hoffmann, Kilian, Leschke, Martin (eds),
Minimal Surfaces: Integrable Systems and Visualisation, m:iv 2017-19;
Springer Proceedings in Mathematics & Statistics 349.
DOI:10.1007/978-3-030-68541-6_3,
EPrint arXiv:2105.08102
Abstract
In this paper, we extend the notion of Schwarz reflection
principle for smooth minimal surfaces to the discrete
analogues for minimal surfaces, and use it to create
global examples of discrete minimal nets with high degree
of symmetry.
- J Cho, K Leschke, Y Ogata (2022)
-
Generalised Bianchi permutability for isothermic surfaces;
Ann Glob Anal Geom 61, 799-829 (2022)
DOI:10.1007/s10455-022-09833-5
Abstract
Isothermic surfaces are surfaces which allow a conformal
curvature line parametrisation. They form an integrable
system, and Darboux transforms of isothermic surfaces obey
Bianchi permutability: for two distinct spectral parameters,
the corresponding Darboux transforms have a common Darboux
transform which can be computed algebraically. In this
paper, we discuss two-step Darboux transforms with the same
spectral parameter, and show that these are obtained by a
Sym-type construction: All two-step Darboux transforms of an
isothermic surface are given, without further integration, by
parallel sections of the associated family of the isothermic
surface, either algebraically or by differentiation against
the spectral parameter.
- J Cho, W Rossman, T Seno (2022)
-
Infinitesimal Darboux transformation and semi-discrete MKDV equation;
Nonlinearity 35(4), 2134 (2022)
DOI:10.1088/1361-6544/ac591f
Abstract
We connect certain continuous motions of discrete planar
curves resulting in semi-discrete potential Korteweg-de
Vries (mKdV) equation with Darboux transformations of smooth
planar curves. In doing so, we define infinitesimal Darboux
transformations that include the aforementioned motions,
and also give an alternate geometric interpretation for
establishing the semi-discrete potential mKdV equation.
- J Dubois, U Hertrich-Jeromin, G Szewieczek (2022)
-
Notes on flat fronts in hyperbolic space;
J Geom 113, 20 (2022)
DOI:10.1007/s00022-022-00628-4
Abstract
We give a short introduction to discrete flat fronts in
hyperbolic space and prove that any discrete flat front in
the mixed area sense admits a Weierstrass representation.
- U Hertrich-Jeromin, G Szewieczek (2022)
-
Discrete cyclic systems and circle congruences;
Annali di Matematica 201, 2797-2824 (2022)
DOI:10.1007/s10231-022-01219-5
Abstract
We discuss integrable discretizations of 3-dimensional
cyclic systems, that is, orthogonal coordinate systems with
one family of circular coordinate lines. In particular,
the underlying circle congruences are investigated in
detail and characterized by the existence of a certain flat
connection. Within the developed framework, discrete cyclic
systems with a family of discrete flat fronts in hyperbolic
space and discrete cyclic systems, where all coordinate
surfaces are discrete Dupin cyclides, are investigated.
- D Polly (2022 PhD thesis)
-
Channel linear Weingarten surfaces in smooth and discrete
differential geometry;
PhD thesis, TU Wien (2022)
Abstract
We consider channel linear Weingarten surfaces in
spaceforms of arbitrary curvature and their discretisation in
the sense of integrable discrete dierential geometry. We use
Lie sphere geometry to unify the dierent ambient spaces.
In the smooth category, we prove that all non-tubular
channel linear Weingarten surfaces are rotational within their
ambient spaceforms. Further we give explicit parametrisations
of all rotational surfaces with constant Gauss curvature
in terms of Jacobi elliptic functions. Thus, we obtain a
transparent classication of all channel linear Weingarten
surfaces in spaceforms with non-negative curvature as well
as a large subclass of channel linear Weingarten surfaces
in hyperbolic spaceforms up to parallel transformation. We
further point out how similar arguments to the ones presented
in this text lead to explicit parametrisations of constant
mean curvature surfaces.
In the discrete category, we advance the theory of
the recently dened class of discrete channel surfaces [U
Hertrich-Jeromin, W Rossman, G Szewieczek: Discrete channel
surfaces; Math Z 294, 747-767 (2020)]. Further, we prove that
all strongly non-tubular discrete channel linear Weingarten
surfaces are rotational within their ambient spaceforms. Also
we outline how this will lead to a classication of large
classes of channel linear Weingarten surfaces, similar to
the results of the smooth theory.
- F Burstall, J Cho, U Hertrich-Jeromin, M Pember, W Rossman (2023)
-
Discrete $\Omega$-nets and Guichard nets via discrete Koenigs nets;
Proc London Math Soc 126(2), 790-836 (2023)
DOI:10.1112/plms.12499
Abstract
We provide a convincing discretisation of Demoulin's
$\Omega$-surfaces along with their specialisations to Guichard
and isothermic surfaces with no loss of integrable structure.
- J Cho, M Pember, G Szewieczek (2023)
-
Constrained elastic curves and surfaces with spherical curvature lines;
Indiana Univ Math J 72(5), 2059-2099 (2023)
DOI:10.1512/iumj.2023.72.9487,
EPrint arXiv:2104.11058
Abstract
In this paper, we consider surfaces with one or two families
of spherical curvature lines. We show that every surface
with a family of spherical curvature lines can locally be
generated by a pair of initial data: a suitable curve of
Lie sphere transformations and a spherical Legendre curve.
We the provide conditions on the initial data for which
such a surface is Lie applicable, an integrable class of of
surfaces that includes cmc and pseudospherical surfaces.
In particular, we show that a Lie applicable surface with
exactly one family of spherical curvature lines must be
generated by the lift of a constrained elastic curve in some
space form. In view of this goal, we give a Lie sphere
geometric characterisation of constrained elastic curves
via polynomial conserved quantities of a certain family
of connections.
- U Hertrich-Jeromin, M Pember, D Polly (2023)
-
Channel linear Weingarten surfaces in space forms;
Beitr Algebra Geom 64, 969-1009 (2023)
DOI:10.1007/s13366-022-00664-w,
EPrint arXiv:2105.00702
Abstract
Channel linear Weingarten surfaces in space forms are
investigated in a Lie sphere geometric setting, which allows
for a uniform treatment of different ambient geometries. We
show that any channel linear Weingarten surface in a space form
is isothermic and, in particular, a surface of revolution in
its ambient space form. We obtain explicit parametrisations for
channel surfaces of constant Gauss curvature in space forms,
and thereby for a large class of linear Weingarten surfaces
up to parallel transformation.
- M Pember, D Polly, M Yasumoto (2023)
-
Discrete Weierstrass-Type Representations;
Discrete Comput Geom 70, 816-844 (2023)
DOI:10.1007/s00454-022-00439-z,
EPrint arXiv:2105.06774
Abstract
Discrete Weierstrass-type representations yield a construction
method in discrete differential geometry for certain classes
of discrete surfaces. We show that the known discrete
Weierstrass-type representations of certain surface classes
can be viewed as applications of the $\Omega$-dual transform
to lightlike Gauss maps in Laguerre geometry. From this
construction, further Weierstrass-type representations
arise. As an application of the techniques we develop,
we show that all discrete linear Weingarten surfaces of
Bryant or Bianchi type locally arise via Weierstrass-type
representations from discrete holomorphic maps.
- S Akamine, H Fujino (2024)
-
Duality of boundary value problems for minimal and maximal surfaces;
Commun Anal Geom 32(4), 1057-1094 (2024)
DOI:10.4310/CAG.241015230035,
EPrint arXiv:1909.00975
Abstract
In 1966, Jenkins and Serrin gave existence and uniqueness
results for infinite boundary value problems of minimal
surfaces in the Euclidean space, and after that such
solutions have been studied by using the univalent harmonic
mapping theory. In this paper, we show that there exists
a one-to-one correspondence between solutions of infinite
boundary value problems for minimal surfaces and those
of lightlike line boundary value problems for maximal
surfaces in the Lorentz-Minkowski spacetime. We also
investigate some symmetry relations associated with the
above correspondence together with their conjugations, and
observe function theoretical aspects of the geometry of these
surfaces. Finally, a reflection property along lightlike
line segments on boundaries of maximal surfaces is discussed.
|
|
Activities
Summer/Autumn school
-
Fukuoka 10-14 Sep 2018
- Vienna 1-5 Oct 2018
Minisymposium at the ICIAM 2019
- Valencia 16-19 Jul 2019
Closing workshop
-
Tokyo 17-21 Feb 2020
People
Birgit Slama (Secretary)
Shintaro Akamine (JP)
Joseph Cho (JP)
Yuta Hatakeyama (JP)
Udo Hertrich-Jeromin (AT)
Yoshiki Jikumaru (JP)
Kenji Kajiwara (JP)
Miyuki Koiso (JP)
Maria Lara Miro (AT)
Kento Okuda (JP)
Hyeongki Park (JP)
Denis Polly (AT)
Florian Rist (AT)
Wayne Rossman (JP)
Yasushi Teruya (JP)
Masaaki Umehara (JP)
Kotaro Yamada (JP)
Links
FWF
- Austrian Science Fund
JSPS
- Japan Society for the Promotion of Science
TUW
- Vienna University of Technology
JASEC
- Japan-Austria Science Exchange Centre
DMG
- Institute of Discrete Mathematics and Geometry
|

 Technische Universität Wien
Technische Universität Wien